某化学工程师想要比较四种油漆混料的硬度。每种油漆混料取六份样品涂到一小块金属上，待金属块凝固后再测量每种样品的硬度。为了检验均值是否相等，并评估均值对之间的差分，分析师配合使用单因子方差分析和多重比较。所以该化学工程师通过对影响质量的因素方面的数据统计，得出了下列数据集合（部分）：

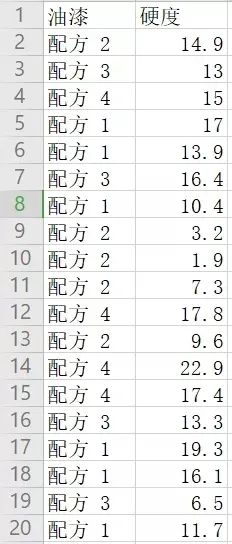
首先,我们需要在数据大脑系统中进行流程的搭建，思路是从数据库中读取数据后，将数据投入到单因素方差分析组件中，然后对算法运行所需要配置的参数进行配置，下图是对数据库读取组件的配置：

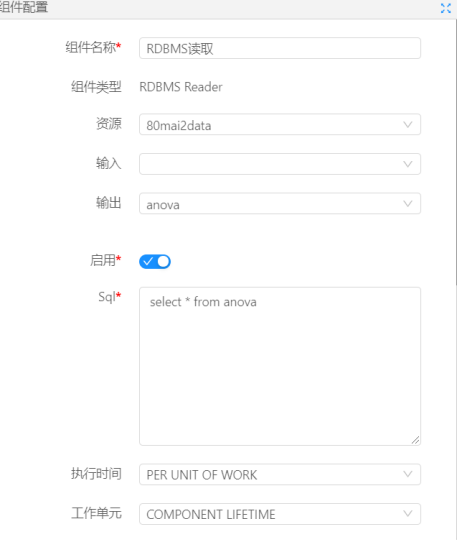
下图是对单因素方差分析组件的配置：

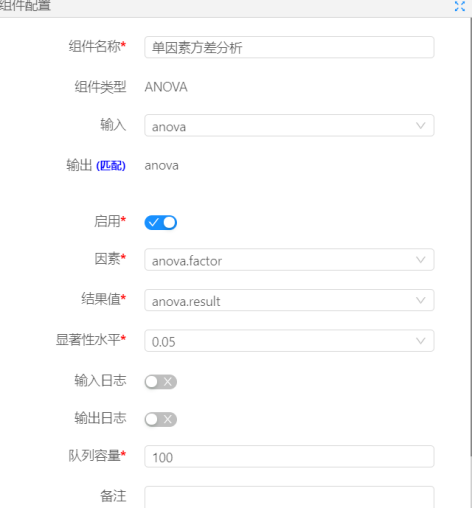
下图是对数据模型的配置：

进行好如此的配置之后，打开调试面板，点击运行，等待系统处理，待运行成功后会在控制台输出结果进行展示。

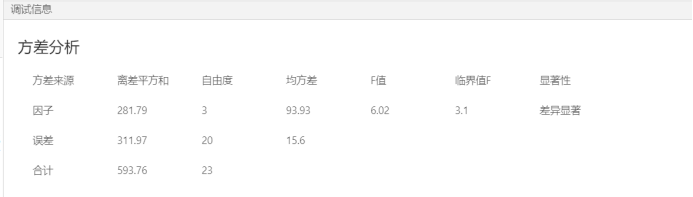
F 值是用于确定项是否与响应相关的检验统计量。F值越大，那么表明项或者模型否定原假设的证据越充分。由于油漆硬度方差分析得到的F值为6.02远大于临界值F=3.1。

我们可以得到的结论是油漆混料的硬度明显不同。据此得出的结论是油漆的配方对油漆混料后的硬度有显著影响，因为单因素方差分析只针对一个因素，所以得出的结果有限，等我们拿到这个数据之后可以在数据大脑平台中进行更进一步的分析，从而可以分析配方的具体哪几种因素对硬度影响较大。

当您有一个类别因子和一个连续响应并且想要确定两个或多个组的总体均值是否存在差异时，可使用单因子方差。

简单来说，如果我想针对一种产品来确认其中的某个因素是不是对我的产品质量有关键性影响，那么我就可以使用单因素方差分析对此进行验证。举个例子来讲，某地毯制造商想要确定几种类型的地毯的耐久性是否存在差异，且这几种类型使用的原料不同，那么我就可以使用单因素方差分析对不同类型的地毯进行分析，来比较最后的地毯耐久度，就可以知道哪种因素对结果影响较大。单因素方差分析的结果我们主要关注的输出点为F值。

在方差分析表中，每个项都显示 F 值：

1.模型或项的 F 值

F 值是用于确定项是否与响应相关的检验统计量。

2.失拟检验的 F 值

F 值是一个检验统计量，用于确定模型是否缺少在当前模型中包含预测变量的高阶项。

如果要使用 F 值来确定是否要否定原假设，请将 F 值与临界值进行比较

总自由度 (DF) 是数据中的信息量。分析使用该信息来估计未知总体参数的值。总自由度由样本中的观测值个数确定。项的自由度显示了项所使用的信息量。增加样本数量可提供有关总体的更多信息，从而增加总自由度。增加模型中项的数量会使用更多信息，这会减少用于估计参数估计值变异性的可用自由度。

均方差又称标准差，简单来说，标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。简单来说，标准差越大，数据越分散。