国工数据大脑之单样本率检验与实验室系统(LIMS) 的融合应用
随着消费者对产品个性化和品质升级的发展需求,制造业的复杂性大大增加,质量检测环节已成为制造业中不可或缺的一部分,目前市面上绝大多数的LIMS系统仅实现或部分实现规范操作,保证质量。而大量的质检数据对研发生产所起的指导作用十分有限,海量数据参数间的相互关系很难被操作人员解读,这也使得杜绝风险,提高交付效率以及为企业创造最大的经济效益成为空谈。国工智能实验室管理系统融合了国工智能数据大脑平台,平台内提供上百种统计学相关算法及机器学习算法。通过这些算法对质检数据进行分类分析、聚类分析、关联分析、预测分析等,挖掘数据潜在价值,探索人力无法探知的规律,真正实现提高企业产品附加值及行业竞争力,助力企业快速发展。
某医疗用品生产企业,对生产的医用防护手套外观有一定要求,要求手套宽度符合≥80mm的标准。抽取10只手套,若有8只宽度都小于80mm,那么我们就会认为实际生产宽度小于80mm,不可采用目前设定的参数进行生产。若抽取10只,仅有1只小于80mm,那么我们并不会认为手套的实际宽度均小于80mm。因为,机器制造手套不可能100%保证每次都是完美的,个别小于80mm是正常现象。所以,我们就可以通过单样本率检验来判断手套的实际生产宽度是否符合外观标准。该手套生产企业一天能生产1万只手套,将一天生产的手套作为整体,通过一定的方法抽样得到50只手套,并对这50只手套的宽度进行检测,宽度小于80mm的记作不合格(本案例需要每隔一段时间抽样5只,共抽样10次来形成样本,以确保抽样的涵盖率),得到50次试验手套宽度的检验结果,如表1所示。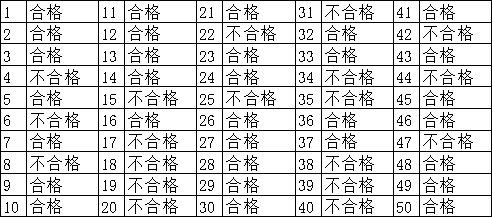
国工数据大脑组件会定时对国工实验室系统数据进行读取,直接访问数据库获取数据集,如图1所示。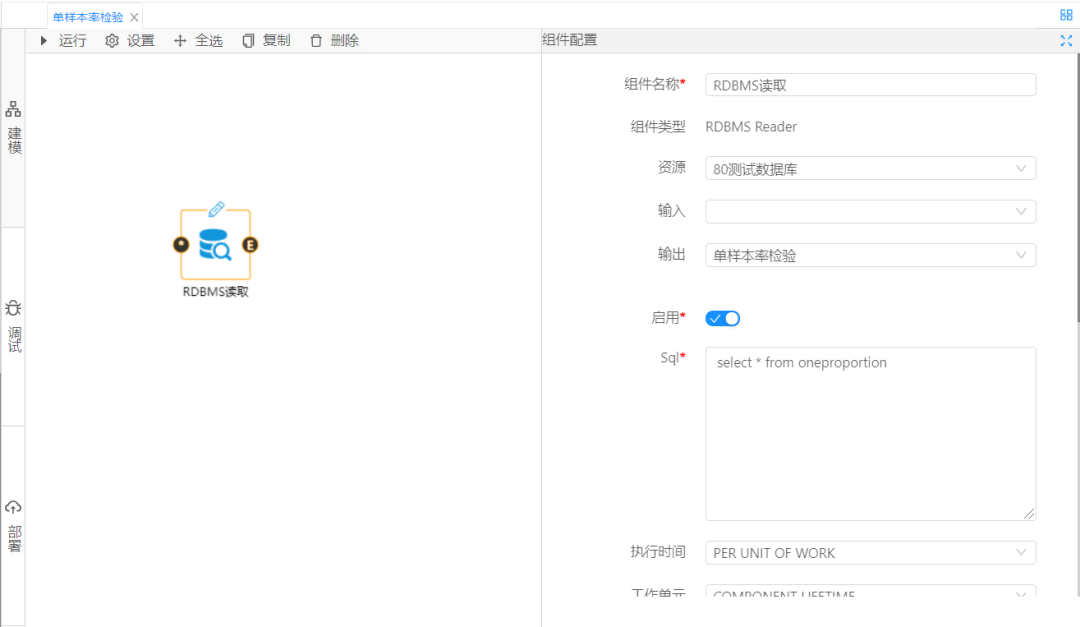
使用集成好算法的单样本率检验分析组件(One-proportion)进行数据的单比率分析处理,根据单样本率假设检验的检验流程:首先确定检验的问题为“手套的实际生产宽度是否符合外观标准”。所以我们将零假设H0设定为手套的实际生产宽度不符合外观标准,那么备择假设H1即可设定为手套的实际生产宽度符合外观标准。我们可以设想,若手套的实际生产宽度≥80mm,则在抽取的50只手套中应只有少量几只手套的宽度小于80mm,如果出现大量手套宽度小于80mm,则我们有理由怀疑手套的实际生产宽度小于80mm。所以,我们假设在抽取的50只手套中仅有2 只不合格的概率为0.01,即设定实验数为50,不合格事件发生数量为2,目标概率为0.01,如图2所示。当然,即使该企业使用当前生产参数生产的手套宽度≥80mm,因为偶然因素导致我们刚好抽取了很多宽度小于80mm的手套的情况也不可避免,此时按照我们的逻辑要拒绝零假设,也就是我们判断错了,我们可以将显著性水平(判断错误的概率)设定为0.05,如图2所示。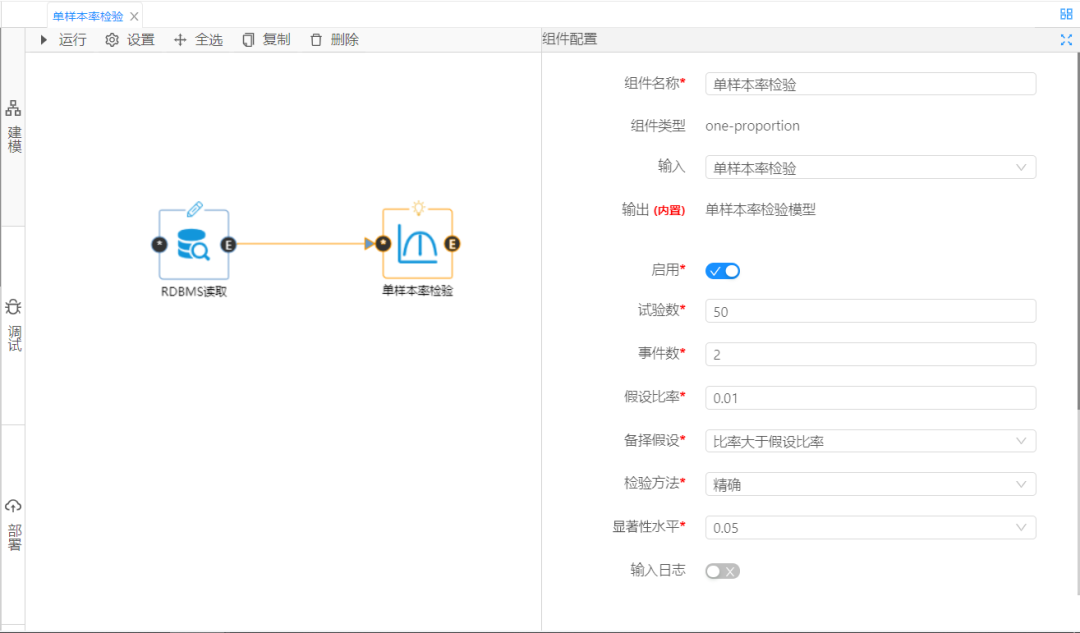

通过图3的系统分析结果,我们可以看到,在上述参数下分析得到的零假设成立概率P为0.014,显然小于显著水平0.05,即原假设(0假设)成立的概率小于判断失误的概率,拒绝原假设,备选成立,该企业手套的实际生产宽度符合外观标准。 国工数据大脑平台可直接获取实验室LIMS系统中的实验数据并将其对接到创建好的单样本率检验分析模型中,根据得出的分析数据自动对检验结果进行判定,快速直接给出判定结果,规避人工审核过程中层层审核的等待时长和判定误差;并将存在显著性差异的报告重点推送给相关领导,系统可根据领导对存在显著性差异报告的处理,自动触发二次检验流程等操作。
实验室系统中的单样本率检验是针对于样本的单一特征,判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征做出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受做出推断,也就是说假设检验的核心思想是小概率事件不易发生。1.试验数:抽取的样本数,如本例中的50只手套。
2.事件数:设定抽取的样本中指定事件发生的次数,如本例中抽取的手套中不合格的有2只。
3.目标比率:设定抽取的样本中指定事件发生某确定次数的理想概率,如本例中抽取的手套中仅有2只不合格的概率为0.01。
4.显著性水平:原假设(0假设)为真时拒绝原假设的概率,通常设定为0.01或0.05,即为小概率事件。
使用单比率检验可以估计二项总体比率,并将该比率与目标值或参考值进行比较。可以在数据的单一特性仅包含两个类别(如合格/不合格)时执行使用此分析,确定总体比率是否不同于指定的假设比率和计算可能包括总体比率的值范围。












