在现代化企业管理中,利用数据分析进行决策支持已成为重要手段,其中包括:过程控制、产能预测、市场决策等等。
在各类业务场景中如何用数字直观地描述指标与指标之间的相关性是一个重要命题,该类业务大多基于回归分析法,回归分析法通过对过去的数据进行采样来构建回归模型,从而为决策和行动提供依据和建议。当回归模型拟合不正确,会误导企业决策的方向,浪费大量人力、物力、财力,给企业造成巨大的损失。因此,对回归模型进行诊断是不可或缺的步骤。即判断回归模型是否正确、理想?换句话说,模型是否很好的提取了样本的规律信息。国工智能MAI平台提供了基于残差检验进行回归模型评估的科学算法。
经典且理想的回归模型的前提条件是:1.随机误差项各项之间无序列相关;2.随机误差项服从正态分布;3.随机误差项方差都相同或是固定的常数。(在实际应用中,随机误差项用残差来代替)
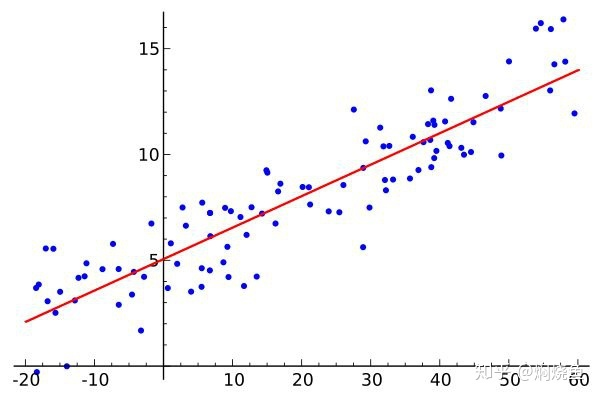
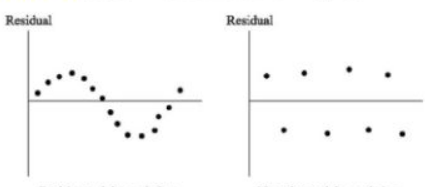
图2 序列正相关
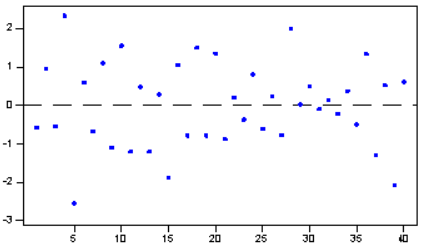
图3 序列不相关
图4
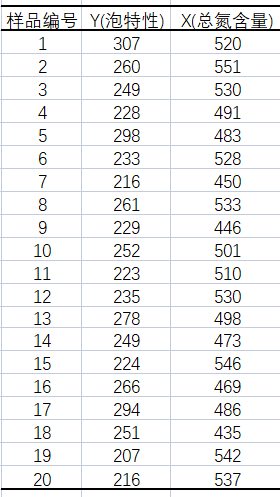
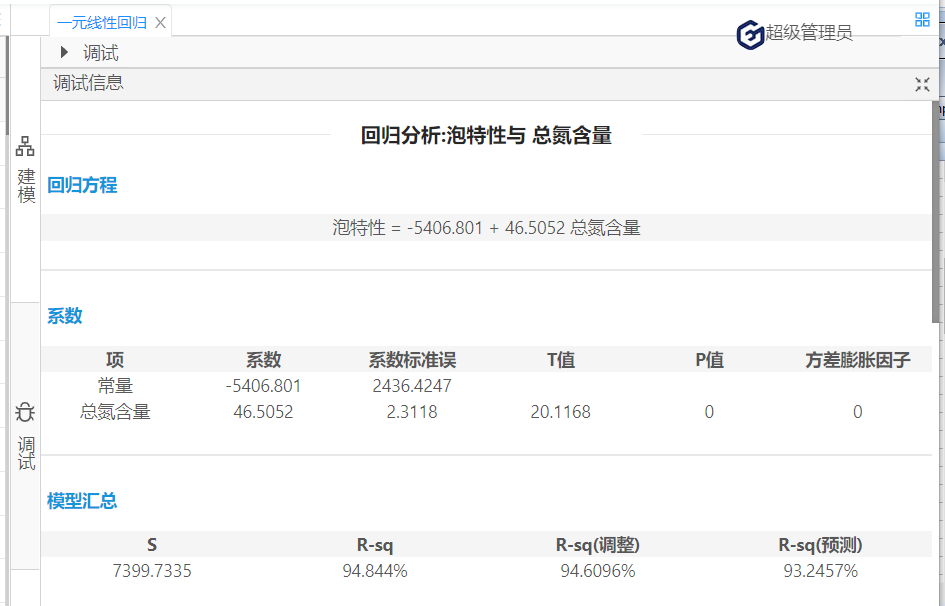
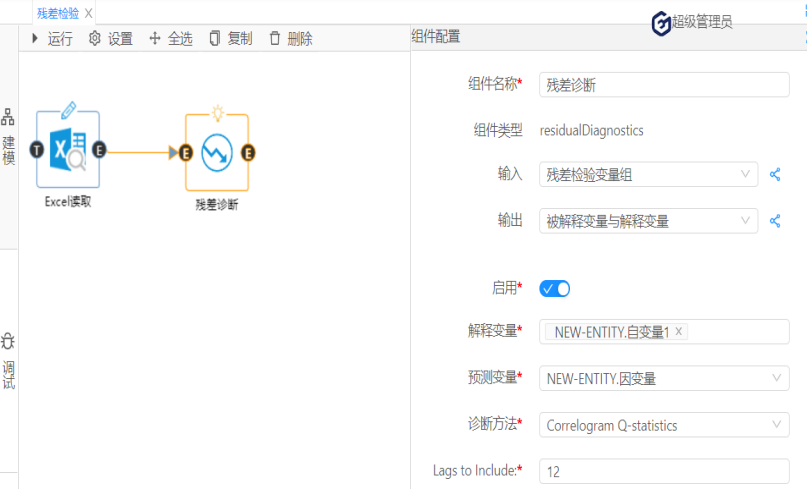
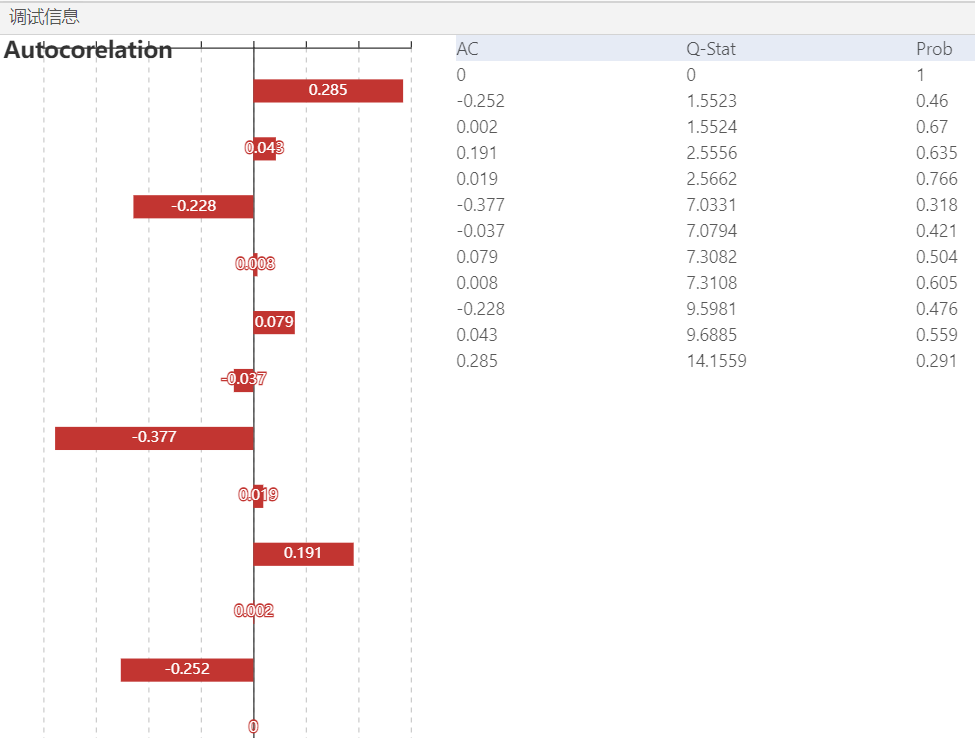
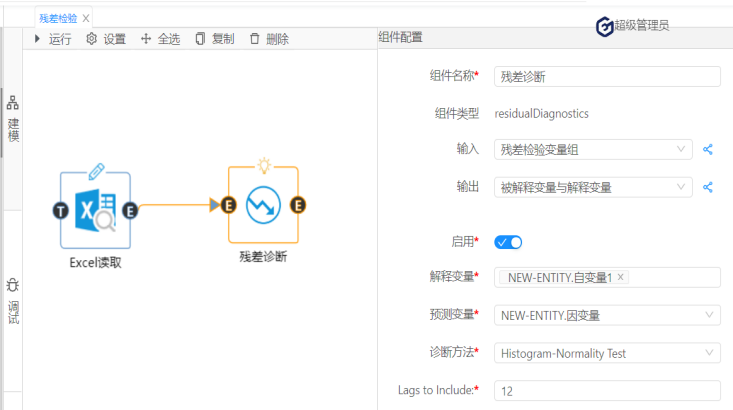
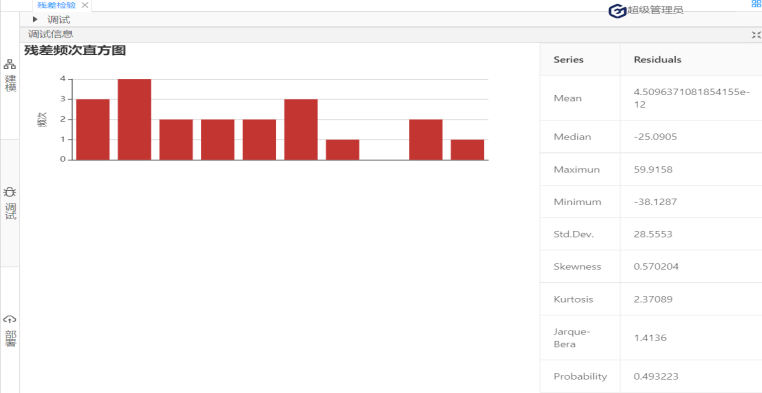
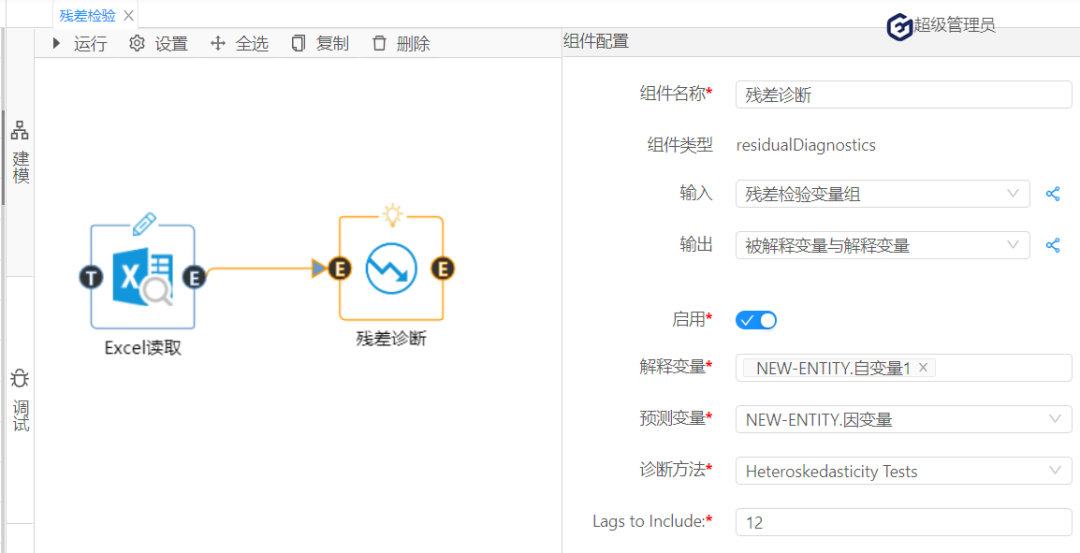
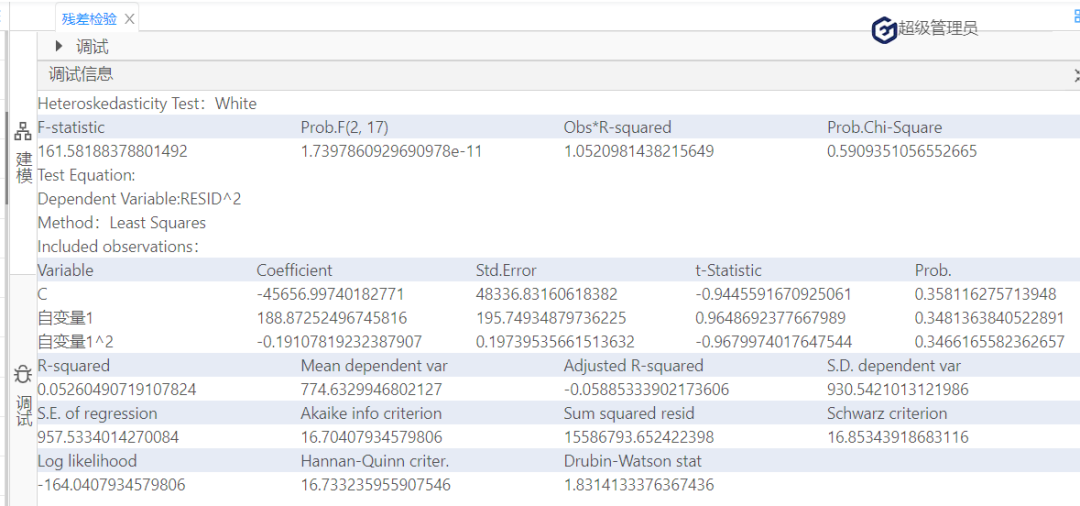
所有线性回归模型。 化工、酿造等装置性行业的过程控制,往往是多变量共同作用。为了做好过程控制,实现“以因素管理结果",我们运用回归分析的统计技术寻找规律,并用于生产过程控制。例如,啤酒酿造过程中成品啤酒的泡特性(秒),是直接关系到啤酒口感的技术要求。技术和经验表明中间产物的总氮含量X对于需要满足的泡沫时间Y (秒)有影响。数据如下: 表1 图5 由图5可知,模型已经通过了统计意义的检验。(具体见国工数据大脑之多元线性回归在化学研发成本的预测一文) 其次,在此基础上,进一步使用数据大脑平台的残差检验算法判断回归模型的理想度。实现残差检验第一个方面:序列相关性的检验。(原假设是:不存在序列自相关。)打开国工数据大脑平台。从数据大脑中的组件面板搜索残差检验组件,拖到到工作面板,配置数据及参数。在诊断方法下拉列表选择:Correlogram-Q-statistics;滞后阶数选择:12。如图6: 图6 运行结果: 图 7 根据图7可知,无论滞后阶数为几,其p值都大于0.1的显著性水平,接受原假设,残差序列不存在序列相关。 接下来,进行残差检验的第二个方面:残差序列正态性检验。(原假设:序列服从正态分布)在诊断方法下拉列表选择:Histigram-Normality-Test;如图3: 图 8 图 9 图10 图11 根据图11可知,怀特检验统计量的值为1.052,它也服从自由度为2的卡方分布,在0.1的显著性水平下,其临界值=4.605,怀特检验统计量值<临界值,接受原假设,该残差序列存在方差相等的情况。 综上,在啤酒的泡特性与总氮含量的一元线性回归模型中,该残差序列不存在序列相关,服从正态分布,且方差相同,上述的三个条件都满足,说明回归模型拟合不错且准确,可使用该模型进行预测。 在下一批生产中,若X(总氮含量)=130,则Y(泡特性)的预测值=-5406.801+46.51*130=639.3(秒),以此类推,能够预测到未来若干次生产中的成品啤酒的泡特性,可通过降低总氮含量等措施控制啤酒的泡特性,从而实现生产控制,实现效益最大化的目标。(具体预测及回归模型含义国工数据大脑多元线性回归在化学研发成本的预测一文)