不管是制造业还是化工行业,对于成本或产量控制、预测、决策都是生产管理中的重要组成部分。以成本控制为例,过去人们对成本控制的认识比较狭隘,传统的成本控制范围局限于制造产品的过程,例如对成本形成过程中一些耗费指标的控制,使它不超过定额预算,如果发生差异,进行差异计算和差异分析,以达到降低成本的目的。所以,传统成本控制重点在生产过程中的差异计算和结束生产过程后的差异分析,是一种消极的成本控制。同时,企业耗费大量人力,物力收集的数据及指标信息并没有得到很好的利用,只是停留在表面的分析。而借助国工数据大脑平台的多元线性回归分析算法,不但可以做到对成本的事先控制,即对企业未来几年的成本进行预测,还可以及早发现企业投入的成本不足或成本过剩的现象,帮助组织明确未来成本需求趋势,做好成本规划工作,从而进行准确决策;而且可以复用历史成本数据深度挖掘出有用的信息,探索出具有一般规律性和普遍适用性的成果。
回归分析是作为数据科学家需要掌握的第一个算法,是数据分析中最基础最重要的分析工具,绝大多数的数据分析问题,都可以使用回归的思想来解决。回归分析的任务就是,通过研究自变量X和因变量Y的数学关系式进而达到通过X去预测Y的目的,它是数据分析中最常用的预测建模技术之一。即使在今天,大多数公司都使用回归技术来实现大规模决策。其中包括了一元线性回归方法、多元线性回归方法和非线性回归方法等。(线性指的是X、Y之间呈线性关系,不管X取什么值,都能在这条回归直线上找到对应的Y,如图1,只要输入X,Y的样本数据,数据大脑中的拟合回归算法就能得到相应的回归直线)
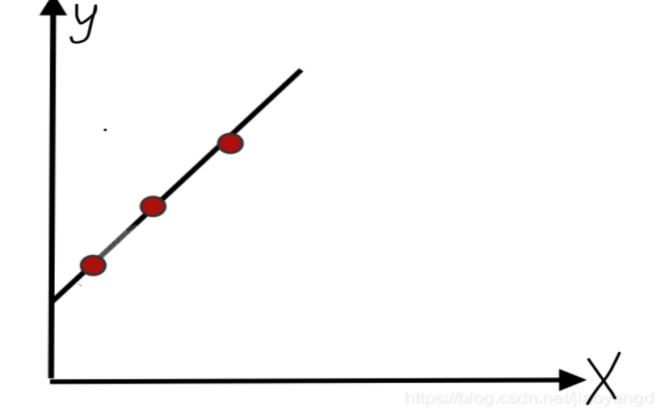
界定线性回归是否为多元,主要看自变量(即X)的个数,若自变量个数在两个及其以上,则称其为多元线性回归,显然若自变量个数有且只有一个,称为一元线性回归。多元线性回归的基本原理和一元线性回归完全相同,区别只在于自变量的个数。
在实际中,一个指标的影响因素通常不止一个,而是有若干个重要因素共同作用才导致事物的发展变化,因此在实际分析时多考虑多元回归分析,本文以较为复杂的多元线性回归为例。多元线性回归模型的一般形式为:
Y=a0+a1*X1+a2*X2+a3*X3…
Y指的是因变量,即我们关注的指标(成本或产量等);X指的是影响Y的因素。a1,a2,a3……指的是影响程度的大小(又称回归系数大小)。
当我们求出回归模型的具体表达式时,还需要进行统计意义检验,通过检验才能使用该模型进行预测。主要包括:拟合优度检验、回归模型的总体显著性检验和回归系数的显著性检验等。 1. 拟合优度检验 拟合优度是指拟合的回归模型与样本观测值之间的接近程度。即衡量一个回归模型做的好不好的指标。用决定系数(R-sq)表示,其数值区间为 0 ~ 1,越接近1,说明模型拟合得越好。判断标准为:大于或等于0.7,认为拟合优度较好;在0.35~0.7之间,认为拟合优度较普通;小于0.35,认为拟合优度较差。 2.回归方程的显著性检验 即检验整个回归方程的显著性,或者说评价所有自变量x整体与因变量Y的线性关系是否密切,整个回归方程本身是否有效。通常采用F检验。 3.回归系数的显著性 若方程通过显著性检验,并不意味着每个自变量对y的影响都显著,所以就需要我们对每个自变量进行显著性检验。若某个自变量系数对y影响不显著,即无关的变量。我们需要从回归方程中将其剔除。通常采用t检验。 成本高低不仅影响着化工行业企业的利润,更是其公司发展壮大的一个制约因素。某有机新材料企业想要减少化学反应中的原料剩余并预测在某种反应参数变量取值下的原料剩余。原料剩余越少,成本利用率越高。把我们想要研究的对象原料剩余(Y)作为因变量,选取了4个主要影响因素:原料A的SM(X1);原料B的硝酸(X2);温度(X3);反应时间(X4)。并进行22次试验。基于22次实验数据进行多元线性回归。 初步得到线性回归方程:Y=a0+a1*X1+a2*X2+a3*X3+a4*X4。 图2
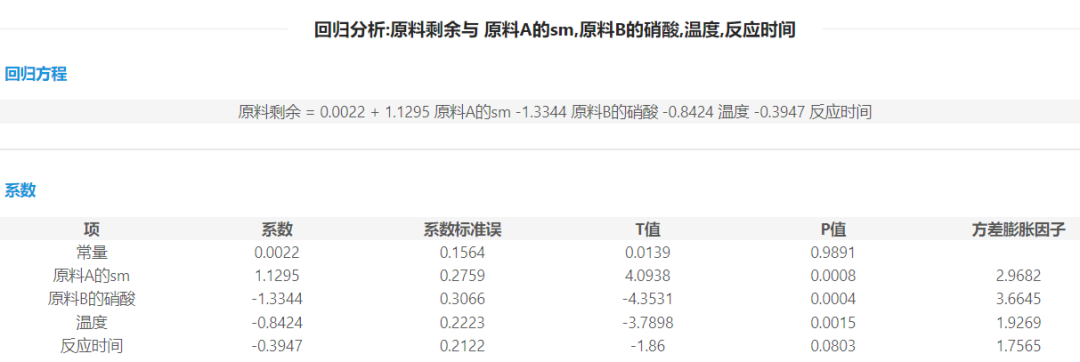
![]()








